Introduction to Multiple Linear Regression

2025-11-17

Housekeeping

  • Study for midterm!
  • Today’s content will not be assessed on midterm, but might be useful for your final project and future coursework!

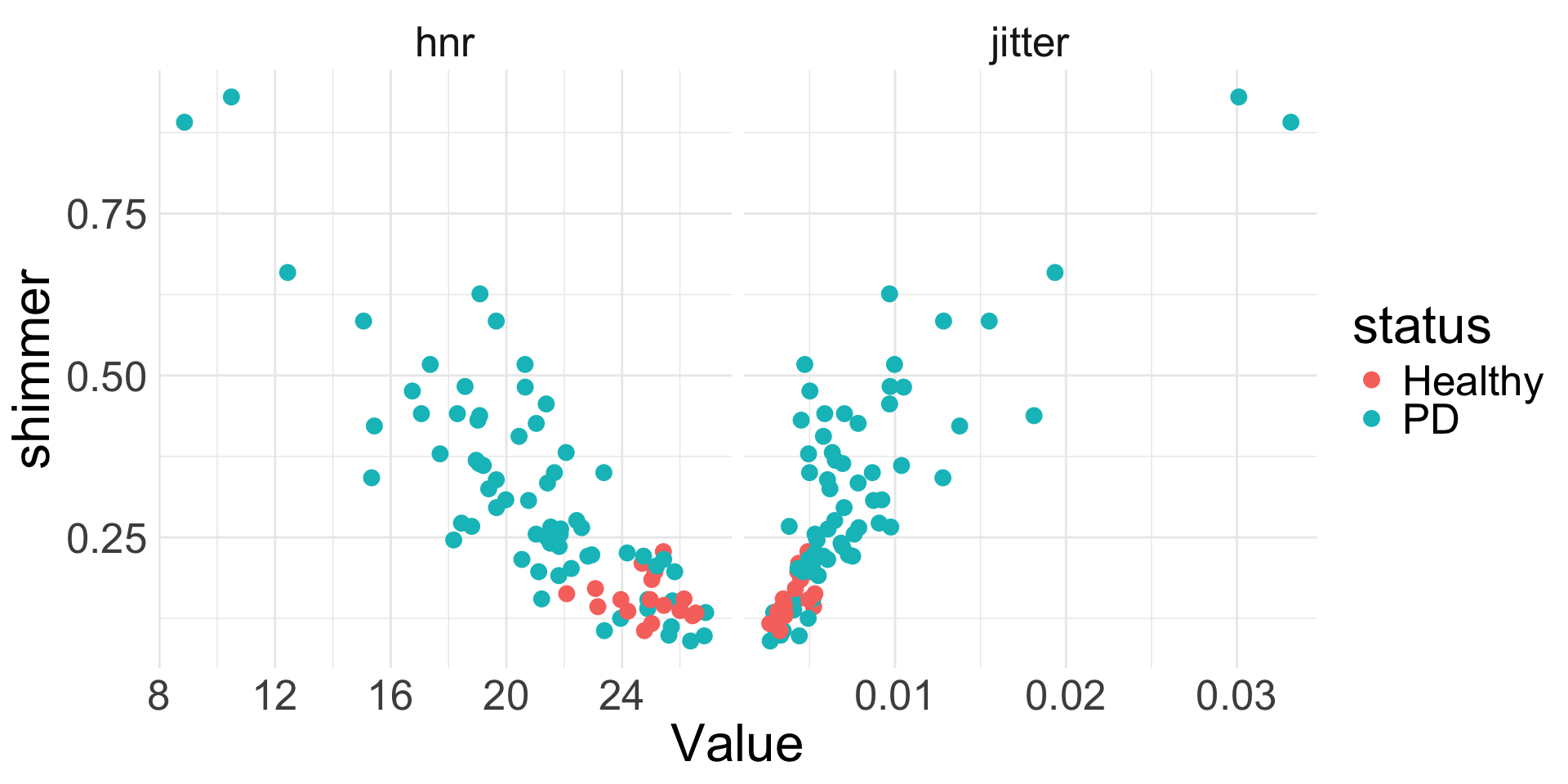
Voice shimmer and jitter data

Recall the data from a previous problem set about voice jitter and shimmer among patients with and without Parkinson’s Disease (PD).

The variables in the dataset are as follows:

  • clip: ID of the recording
  • jitter: a measure of variation in fundamental frequency
  • shimmer: a measure of variation in amplitude
  • hnr: a ratio of total components vs. noise in the voice recording
  • status: PD vs. Healthy
  • avg.f.q: 1, 2, or 3, corresponding to average vocal fundamental frequency (1 = low, 2 = mid, 3 = high)

Analysis goal

Want to understand what might help explain the voice shimmer of a patient with low vocal fundamental frequency.

  • What do you notice about how shimmer relates to hnr, jitter, and status?

  • Can we somehow incorporate all the predictors into the same model for shimmer? Do you think we need to?

Multiple linear regression

Multiple linear regression

  • We have seen simple linear regression, where we had one explanatory variable

  • Extend to include multiple explanatory variables

    • Seems natural: usually several factors affect behavior of phenomena

  • Multiple linear regression takes the form: \[y = \beta_{0} + \beta_{1} x_{1} + \beta_{2} x_{2} + \ldots + \beta_{p} x_{p} + \epsilon\]

    • Now there are \(p\) different explanatory variables \(x_{1},\ldots, x_{p}\) per observation

    • Still one response \(y\) and error \(\epsilon\) per observation

  • Represents a holistic approach for modeling all of the variables simultaneously

PD data (cont.)

Let’s start off by building a model that does not include status, as the EDA didn’t seem to show a strong relationship between status and shimmer.

  • Our multiple linear regression model is:

    \[\text{shimmer} = \beta_{0} + \beta_{1} \text{hnr} + \beta_{2} \text{jitter} + \epsilon\]

  • Just as in the case of SLR, the estimates of \(\beta_{0}, \beta_{1}, \beta_{2}\) parameters are chosen via the least squares criterion

Multiple regression in R

Very easy to code:

shimmer_lm <- lm(shimmer ~ hnr + jitter, data = pd)
tidy(shimmer_lm)
term estimate std.error statistic p.value
(Intercept) 0.732 0.091 8.022 0.0000000
hnr -0.025 0.004 -7.066 0.0000000
jitter 13.467 2.574 5.232 0.0000012

  • Simply identify the estimated coefficients from the output to obtain fitted model

  • Try writing down the fitted model

\[ \begin{align*} \widehat{\text{shimmer}} &= 0.732 -0.025 \text{hnr}+ 13.467 \text{jitter} \end{align*} \]

  • FOR NOW: assume conditions are met just for sake of interpretation practice

Interpretation of intercept

  • Interpretation of the estimated intercept \(b_{0}\) in MLR is very similar to SLR!

\[ \begin{align*} \widehat{\text{shimmer}} &= 0.732 -0.025 \text{hnr} + 13.467 \text{jitter} \end{align*} \]

  • Try interpreting the intercept!

  • We simply plug in 0 for all the explanatory variables

    • The estimated voice shimmer of a patient with 0 hnr and 0 voice jitter is 0.732.

Interpretation of non-intercept

  • When we have more than one predictor variable, interpretation of the coefficients requires a bit of care

    • Multiple moving parts

  • Interpretation of a particular non-intercept coefficient \(b_{k}\) relies on “holding the other variables fixed/constant” (assuming the model is appropriate)

\[ \begin{align*} \widehat{\text{shimmer}} &= 0.732 -0.025 \text{hnr} + 13.467 \text{jitter} \end{align*} \]

  • For every one unit increase in a person’s HNR, their voice shimmer is expected/estimated to \(\color{orange}{\text{decrease by } 0.025}\), holding their voice jitter value constant

  • Interpret the coefficient associated with jitter

Interpretation of non-intercept (cont.)

\[ \begin{align*} \widehat{\text{shimmer}} &= 0.732 -0.025 \text{hnr} + 13.467 \text{jitter} \end{align*} \]

  • For every one unit increase in a patient’s voice jitter, their voice shimmer is expected to \(\color{orange}{\text{increase by } 13.467}\) units, holding their HNR value constant

More isn’t always better

  • You might be tempted to throw in all available predictors into your model! Don’t fall into temptation!

  • Quality over quantity

  • For SLR, we used the coefficient of determination \(R^2\) to assess how good the model was

    • \(R^2\) is less helpful when there are many variables

    • Why? The \(R^2\) will never decrease (and will almost always increase) when we include an additional predictor

Adjusted \(R^2\)

  • For multiple linear regression, we use the adjusted \(R^2\) to assess the quality of model fit

    • “Adjusted” for the presence of additional predictors

    • Take STAT 211 to learn the formula and intuition behind it!

  • Adjusted \(R^2\) is always less than \(R^2\), and doesn’t have a nice interpretation

  • When choosing between models, one method is to choose the one with highest adjusted \(R^2\)

Adjusted \(R^2\) (cont.)

summary(shimmer_lm)

Call:
lm(formula = shimmer ~ hnr + jitter, data = pd)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.182276 -0.047886 -0.007739  0.029861  0.236647 

Coefficients:
             Estimate Std. Error t value         Pr(>|t|)    
(Intercept)  0.732203   0.091279   8.022 0.00000000000589 ***
hnr         -0.024795   0.003509  -7.066 0.00000000045372 ***
jitter      13.466902   2.573728   5.232 0.00000123460798 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.07437 on 83 degrees of freedom
Multiple R-squared:  0.807, Adjusted R-squared:  0.8024 
F-statistic: 173.5 on 2 and 83 DF,  p-value: < 0.00000000000000022
glance(shimmer_lm)
r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC deviance df.residual nobs
0.807 0.8024 0.0744 173.5385 0 2 102.9875 -197.975 -188.1576 0.4591 83 86

Conditions for inference

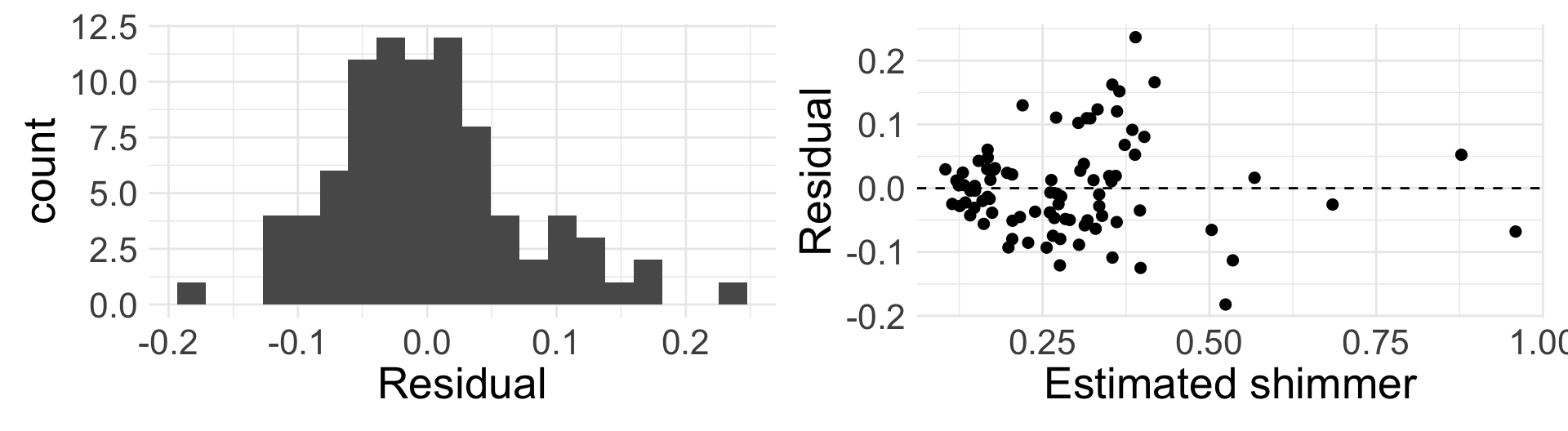
We still need LINE to hold

  • Linearity: harder to assess now that multiple predictors are involved. Good idea to make several scatter plots

  • Independence: same as before

  • Nearly normal residuals: same as before

  • Equal variance: because we have multiple explanatory variables, residual plot in MLR has fitted values \(\hat{y}\) on the x-axis

Inference in MLR

Hypothesis testing in MLR

  • In MLR, we are interested in the effect of each predictor variable on response \(y\)

    • Need to account for presence of other predictors in the model

  • \(H_{0}: \beta_{k} = 0\), given other predictors in the model

  • \(H_{A}: \beta_{k} \neq 0\), given other predictors in the model (or \(>, <\))

  • We can write down one null hypothesis for each coefficient in the model

Hypothesis tests from lm()

\[\text{shimmer} = \beta_{0} + \beta_{1} \text{hnr} + \beta_{2} \text{jitter} + \epsilon\]

We can test the following null hypotheses (no need to write down):

  • \(H_{0}: \beta_{1} = 0\), given jitter is included in the model
    • i.e. HNR has no effect on shimmer once we account for jitter
  • \(H_{0}: \beta_{2} = 0\), given HNR is included in the model

Hypothesis tests from lm()

term estimate std.error statistic p.value
(Intercept) 0.73 0.091 8.022 0.0000000
hnr -0.02 0.004 -7.066 0.0000000
jitter 13.47 2.574 5.232 0.0000012

  • Output from lm() provides:

    • Test statistic, which follows \(t_{n-q}\) where \(q =\) total number of unknown coefficients (i.e. \(\beta\) terms)

    • p-values for testing two-sided \(H_{A}\) provided

Based on the model fit, which variables seem to be important predictors of voice shimmer? Why?

Hypothesis tests from lm() (cont.)

term estimate std.error statistic p.value
(Intercept) 0.732 0.091 8.022 0.0000000
hnr -0.025 0.004 -7.066 0.0000000
jitter 13.467 2.574 5.232 0.0000012

  • HNR does seem to be an important predictor for voice shimmer, even when including jitter in the model

    • Low p-value suggests it would be extremely unlikely to see data that produce \(b_{1} = -0.025\) if the true relationship between shimmer and HNR was non-existent (i.e., if \(\beta_{1} = 0\)) and the model also included jitter

  • Jitter does seem to be an important predictor, even when including HNR in the model

More complex model

Let’s see a model that now includes the status of the patient as a predictor:

shimmer_lm2 <- lm(shimmer ~ hnr + jitter + status, data = pd)
tidy(shimmer_lm2)
term estimate std.error statistic p.value
(Intercept) 0.688 0.103 6.668 0.0000000
hnr -0.024 0.004 -6.273 0.0000000
jitter 13.662 2.585 5.285 0.0000010
statusPD 0.020 0.022 0.915 0.3628131
  • Remember, status is categorical with two levels. lm() converted to indicator variable for us: statusPD = 1 when status = "PD"

Write out the fitted model.

Interpretation with categorical variable

\[ \widehat{\text{shimmer}} = 0.688 -0.024 \text{hnr} + 13.662 \text{jitter} + 0.02 \text{statusPD} \]

  • Try interpreting the intercept here!

  • What does it mean for the explanatory variables to be 0? It means hnr = 0, jitter = 0, and the patient does not have PD

    • A “healthy” patient with HNR and jitter values of 0 is estimated to have a voice shimmer of 0.688

Interpretation of slope coefficients

\[ \widehat{\text{shimmer}} = 0.688 -0.024 \text{hnr} + 13.662 \text{jitter} + 0.02 \text{statusPD} \]

Try interpreting the coefficients of hnr, jitter, and statusPD. Remember the special wording/acknowledgement now that we are in MLR world!

  • Coefficient for hnr: for every one unit increase in HNR, we expect the patient’s shimmer to decrease by 0.024 units, holding the other variables (jitter and status) constant.

  • Coefficient for jitter: for every one unit increase in jitter, we expect the patient’s shimmer to increase by 13.662 units, holding the other variables constant.

  • Coefficient for statusPD: patients with PD are estimated to have a voice shimmer 0.02 units higher than patients without PD, holding the other variables constant

Effect of status

term estimate std.error statistic p.value
(Intercept) 0.688 0.103 6.668 0.0000000
hnr -0.024 0.004 -6.273 0.0000000
jitter 13.662 2.585 5.285 0.0000010
statusPD 0.020 0.022 0.915 0.3628131

Based off the model output, does it appear that status is an important predictor of a patient’s voice shimmer? Why or why not? What about the other two variables hnr and jitter?

Comparing models

Let’s compare the two models:

tidy(shimmer_lm) |>
  select(term, estimate, p.value)
term estimate p.value
(Intercept) 0.732 0.000000
hnr -0.025 0.000000
jitter 13.467 0.000001 
glance(shimmer_lm)
r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC deviance df.residual nobs
0.807 0.8024 0.0744 173.5385 0 2 102.9875 -197.975 -188.1576 0.4591 83 86 
tidy(shimmer_lm2) |>
  select(term, estimate, p.value)
term estimate p.value
(Intercept) 0.688 0.000000
hnr -0.024 0.000000
jitter 13.662 0.000001
statusPD 0.020 0.362813 
glance(shimmer_lm2)
r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC deviance df.residual nobs
0.809 0.802 0.0744 115.7449 0 3 103.4244 -196.8488 -184.5771 0.4544 82 86

What do you notice about the estimated coefficients, \(R^2\), and adjusted \(R^2\) across the two models?

Remarks

  • We have only scratched the surface of MLR

  • Things to consider (beyond our course):

    • Multicollinearity (when the predictor variables are correlated with each other)

    • Model selection

    • More than one categorical variable

    • Interaction effects